Día Mundial de Fibonacci, en honor al descubridor del número áureo
Este número tiene una amplia presencia en la naturaleza, como así también ha sido utilizada históricamente en la arquitectura, el arte y el diseño.

El 23 de noviembre se celebra el Día Mundial de Fibonacci en honor al matemático italiano Leonardo de Pisa, también conocido con el nombre de Fibonacci.
Además de introducir el sistema decimal en Europa, hoy se lo recuerda por ser el descubridor de una secuencia numérica que representa la misma belleza: la sucesión de Fibonacci, también conocida como proporción áurea o número áureo.
La sucesión de Fibonacci es una secuencia de números que resultan al sumar los dos anteriores a ese. Empezando desde 0, tenemos la siguiente: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 ... y así sucesivamente.
Esta relación matemática tiene una amplia presencia en la naturaleza, en los patrones que adornan los pétalos de las flores, las espirales de las conchas marinas o, incluso, las ramificaciones de los árboles, se encuentra la elegante y misteriosa proporción áurea.

Es un concepto que ha llamado la atención a matemáticos, artistas, filósofos y científicos a lo largo de la historia, llegando a influir de manera notable en el arte y la arquitectura, como es el caso de la Mona Lisa de Leonardo da Vinci, o de la estructura del Partenón de Atenas, debido a su asociación con la belleza y la armonía visual.
Se eligió la fecha del 23 de noviembre porque corresponde a los primeros dígitos de la sucesión en escritura anglosajona 11/23.
EL NÚMERO DORADO
El número dorado, el número de Dios, el número divino, phi … El número áureo responde ante múltiples nombres que lo hacen parecer una de las cifras más importantes y emblemáticas de las matemáticas, pero ¿a qué hace referencia realmente? Pues, numéricamente, no es más que la relación entre dos segmentos de una recta, es decir, una simple proporción geométrica (proporción áurea).
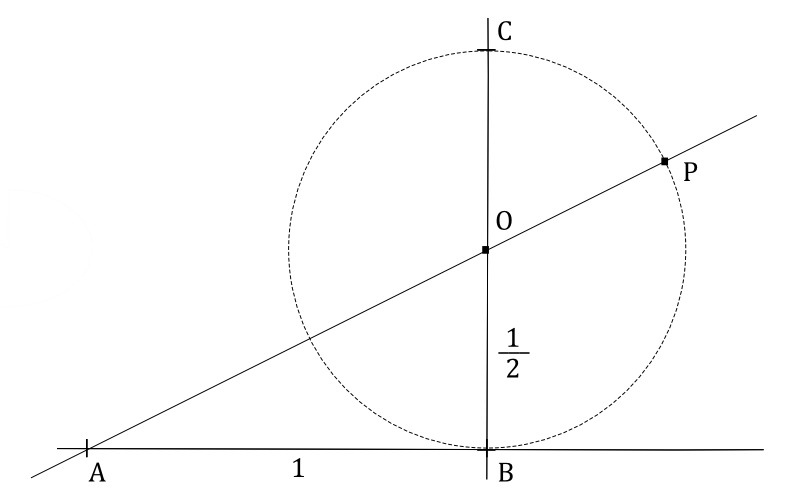
Se trata de un número irracional, o lo que es lo mismo, que no puede expresarse como razón de dos números enteros y, por lo tanto, es infinito: siempre se puede calcular alguna cifra más y no tiene un valor final. El valor numérico al que responde es el 1.618033988…
LA PROPORCIÓN ÁUREA
Una forma de entender mejor cómo funciona la proporción áurea es a través de la sucesión de Fibonacci, una serie de cifras en la que la suma de dos números consecutivos siempre da como resultado el siguiente y, además, la relación entre cada número se aproxima siempre al número de áureo. Es decir, la sucesión se define como: 0,1,1,2,3,5,8,13,21,34… donde el tercer número es la suma del primero y el segundo, el cuarto es la suma del segundo y el tercero, el quinto es la suma del tercero y el cuarto… Y para encontrar el número áureo solo tenemos que dividir cada número entre el anterior, eso sí, mejor que empieces en el 5, pues debes dejar a la sucesión formarse bien.
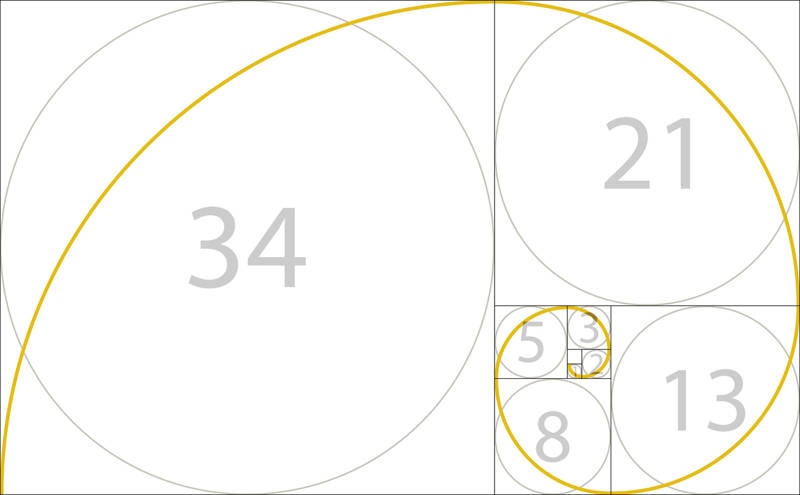
¿Y te suena la espiral áurea? Pues ese elemento es la “aplicación práctica" de nuestra proporción. Para encontrar la espiral debes imaginar un rectángulo y trazar un cuadrado dentro que divida al rectángulo en dos partes no iguales. Luego, debes trazar otro cuadrado en la parte pequeña, y así sucesivamente. Los lados de los cuadrados representarán cada uno de los valores de la sucesión (los dos más pequeños tendrían lado de magnitud 1, el siguiente 2, luego 3 y después 5…) La espiral saldrá del cuadrado más pequeño y atravesará la mitad del cuadrado con una curva.
EL NÚMERO ÁUREO EN LA NATURALEZA
Sin embargo, lo más increíble de este patrón, no es quizás toda esa parte matemática, sino la forma en la que aparece de manera constante en la naturaleza, dejando huella en múltiples sistemas vegetales, animales e incluso humanos. El ejemplo más reconocido es el de las conchas de animales marinos: existen diversas especies de nautilus, propias de la familia Nautiliade donde la proporción entre las espiras del interior de la concha responde a la proporción áurea, siguiendo la trayectoria marcada por la espiral.

Otros ejemplos de lo más llamativos son la distribución de los pétalos de ciertas flores, la cantidad de espirales con las que consta una piña o la relación entre el grosor de las ramas principales de un árbol y su tronco. Además, en los girasoles es muy evidente apreciar la famosa espiral áurea en su parte central, justo en las semillas colocadas entre las flores.
Los humanos no se salvan. El ejemplo más curioso es que, para cada individuo, el número áureo aparece como la relación de la distancia entre el ombligo y la planta, con la altura total. Además, la belleza de la proporción influye sobre la forma en que percibimos si una persona es “más o menos guapa” pues, cuanto más se acerque su cara a la distribución áurea, más prototípicamente bellas nos parecerán sus facciones.

EL NÚMERO ÁUREO EN EL ARTE Y LA ARQUITECTURA
La observación de esa proporción divina en los sistemas naturales a lo largo de los años, supuso una clara influencia para diversos artistas, los cuales decidieron incluirla en sus obras y creaciones. Muchas de ellas pasaron a la historia y se presentan hoy en día como cuadros, sinfonías u obras arquitectónicas de lo más emblemáticas. Un claro ejemplo es la pirámide de Guiza: la altura del monumento dividida por la mitad de la base es aproximadamente igual al número áureo. Además, las secciones en las que se divide la pirámide, como la altura hasta el punto medio y la cúspide, responderían también de acuerdo a la proporción.

La Mona Lisa es quizás la obra más reconocida que cumple la proporción áurea, aunque también aparece en esa lista el cuadro Leda atómica de Dalí, la cual destaca por haber sido pintada con el asesoramiento del matemático Matila Ghyka. En la obra de da Vinci, destaca sobre todo la forma en la que los patrones faciales se asemejan a la proporción áurea, o la comparación del aspecto rectangular del retrato con la relación áurea. Incluso, algunos investigadores han identificado curvas dentro de la pintura que se asemejan a las espirales áureas.
En arquitectura se destacaría también el Partenón de Atenas debido a la relación que aparece entre las medidas del techo y las columnas, o los violines, pues su diseño implica que la ubicación de sus “eses” se relacione directamente con la proporción áurea. Incluso en la música es posible encontrar el número divino, como es el caso de las estructuras formales que aparecen en las sonatas de Wolfgang Amadeus Mozart, o en la Quinta Sinfonía de Ludwig van Beethoven. Sin embargo, los expertos optan por la idea de que ambas se compusieron, probablemente, basándose en el equilibrio de masas sonoras, no siendo realmente conscientes los autores de la utilización de la proporción.
SudOeste B.A. con información de National Geographic















